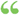 Divide the first term of the remainder by three times the square of the root already found, and write the quotient for the next term of the root. Divide the first term of the remainder by three times the square of the root already found, and write the quotient for the next term of the root.  Elements of Algebra - Side 2281838 - 355 siderUten tilgangsbegrensning Elements of Algebra - Side 2281838 - 355 siderUten tilgangsbegrensning - Om denne boken
 | Charles Davies - 1835 - 378 sider
...II. Divide the second term of N by three times the square of the first term of R : the quotient will be the second term of R. III. Having found the two...which, divide the first term of the remainder by three limes the square of the first term of R .- the quotient will be the third term of R. IV. Cube the three... | |
 | James Bryce - 1837 - 322 sider
...cube root of the first term, and subtract its cube from the given quantity; 3* take the quotient of the first term of the remainder by three times the square of the part of the root already found, and set it down as the next term of the root: then, to the treble of... | |
 | Charles Davies - 1842 - 368 sider
...Therefore, having arranged RULE. I. Extract the cube root of the first term. II. Divide the second term of N by three times the square of the first term of R : the quotient mil be the second term of R. III. Having found the two first terms of R,form the cube of the binomial... | |
 | Charles Davies - 1845 - 382 sider
...root, the following KULE. I. Extract the cube root of the first term. II. Divide the second term of N by three times the square of the first term of R; the quotient will be the second term of R. III. Having found the first two terms of R, form the cube of this binomial and subtract... | |
 | Ormsby MacKnight Mitchel - 1845 - 308 sider
...of the root, cube the root already found, subtract it from the power, and bring down the remainder ; divide the first term of the remainder by three times the square of the root already found, and the quotient will be the second term of the root. To get the third term of... | |
 | Elias Loomis - 1846 - 376 sider
...some one letter, take the cube root of the first term, and subtract the cube from the given quantity. Divide the first term of the remainder by three times the square of the root already found, the quotient will be the second term of the root. Complele the divisor by adding... | |
 | Elias Loomis - 1846 - 380 sider
...some one letter, take the cube root of the first term, and subtract the cube from the given quantity. Divide the first term of the remainder by three times the square of the root already found, the quotient will be the second term of the root. Complete the divisor by adding... | |
 | 1847 - 386 sider
...term of R. [II. Having found the. ßrst two terms of R, form the cube of this binomial and subtract il from N ; after which, divide the first term of the remainder by three times the square of the ßrst term of R : the quotient will be the third term of R. IV. Cube the three terms of the root found,... | |
 | Stephen Chase - 1849 - 348 sider
...first term of the root into another term. We may, therefore, iind another term of the root by dividing the first term of the remainder by three times the square of the first term of the root. See § 169. c.) If now we subtract from the given polynomial the cube of the part of the... | |
 | Benjamin Greenleaf - 1852 - 348 sider
...; but 3a?b+3ab2+b a =(3a?-\-3ab+b2)b. It is therefore manifest, that b will be obtained by dividing the first term of the remainder by three times the square of a ; and, to complete the divisor, we must add to 3a 2 three times the product of the two terms, or... | |
| |