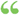 C' (89) (90) (91) (92) (93) 112. In any plane triangle, the sum of any two sides is to their difference as the tangent of half the sum of the opposite angles is to the tangent of half their difference.  A Treatise of Practical Surveying, ... - Side 94av Robert Gibson - 1808 - 440 siderUten tilgangsbegrensning - Om denne boken
 | William Mitchell Gillespie - 1869 - 550 sider
...to each other at the opposite sides. THEOREM EL — In every plane triangle, the turn of two tides is to their difference as the tangent of half the sum of the angles opposite those sides is to the tangent of half their difference. THEOREM III. — In every plane... | |
 | New-York Institution for the Instruction of the Deaf and Dumb - 1869 - 698 sider
...we have the principle. When two sides and their included angles are given : The sum of the two sides is to their difference as the tangent of half the sum of the other two angles is to the tangent of half their difference. This young man also worked out a problem... | |
 | Charles Davies - 1870 - 392 sider
...0 : sin B. Theorems. THEOREM II. In any triangle, the sum of the two sides containing either angle, is to their difference, as the tangent of half the sum of the two other angles, to the tangent of half their difference. Let ACB be a triangle: then will AB + AC: AB—... | |
 | New-York Institution for the Instruction of the Deaf and Dumb - 1871 - 370 sider
...we have the principle. When two sides and their included angles are given : The sum of the two sides is to their difference as the tangent of half the sum of the other two angles is to the tangent of half their difference. This young man also worked out a problem... | |
 | Elias Loomis - 1871 - 302 sider
...^(A+B) . sin. A-sin. B~sin. ^(AB) cos- ^(A+B)~tang. ^(AB) ' that is, The sum of the sines of two arcs is to their difference, as the tangent of half the sum of those arcs is to the tangent of half their difference. COS f*fvt Dividing formula (3) by (4), and considering... | |
 | Charles Davies - 1872 - 464 sider
...have the following principle : In any plane triangle, the sum of the sides including either angle, is to their difference, as the tangent of half the sum of the two other angles, is to the tangent of half their difference. The half sum of the angles may be found by... | |
 | Edward Olney - 1872 - 472 sider
...horizontal parallax. PLANE TRIGONOMETRY. 80. Ргор.— The sum of any two sides of a plane triangle is to their difference, as the tangent of half the sum of the angles opposite is to the tangent of half their difference. ( DEM. — Letting a and b represent any... | |
 | William Frothingham Bradbury - 1872 - 262 sider
...same sine, and BD = a sin. BCD = a sin. C (41) B 102. In any plane triangle, the sum of any two sides is to their difference, as the tangent of half the sum of the opposite angles is to the tangent of half their difference. Let ABC (Art. 103) be a plane triangle... | |
 | Edward Olney - 1872 - 216 sider
...horizontal parallax. PLANE TRIGONOMETRY. 86. Prop.— Tlie sum of any two sides of a plane triangle is to their difference, as the tangent of half the sum of the angles opposite is to the tangent of half their difference. DEM. — Letting a and b represent any... | |
 | Edward Olney - 1872 - 562 sider
...horizontal parallax. PLANE TRIGONOMETRY. 86. Prop.— TJie sum of any two sides of a plane triangle is to their difference, as the tangent of half the sum of the angles opposite is to the tangent of half their difference. 1 >K\r. — Letting a and b represent any... | |
| |
